最是琐事磨人耐性
搜索策略
引言
 ## 盲目搜索
## 盲目搜索
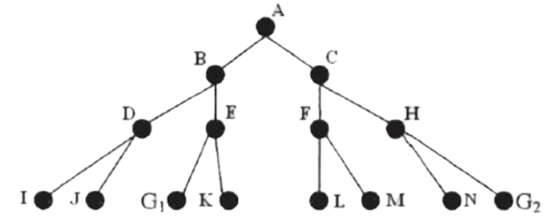
宽度优先搜索(BFS)
OPEN表中简单的排序方式:扩展但花钱节点后生成的子结点总是置于OPEN表的后端,即OPEN表作队列,先进县出,使搜索优先横向发展。 宽度优先算法可以表示为如下步骤: 1. 把初始节点放入OPEN表。 2. 若OPEN表为空则问题无解,失败并退出。 3. 把OPEN表的第一个节点去除放入CLOSE表中并按照顺序冠以编号n。 4. 考察节点n不可扩展则转到第2步。 5. 否则扩展节点n将其子结点防盗OPEN表的尾部,并为每一个子节点都配置指向夫节点的指针,然后转第2步。
| OPEN表 | CLOSE表 |
|---|---|
| [A] | [] |
| [B,C] | [A] |
| [C,D,E] | [B,A] |
| [D,E,F,H] | [C,B,A] |
| [D,E,F,H,I,J] | [D,C,B,A] |
| [D,E,F,H,I,J, ,K] | [E,D,C,B.A] |
| [H,I,,K,L,M] | [F,E,D,C,B,A] |
… 直到出现在OPEN表的最后
深度优先搜索(DFS)
OPEN表中的排序方式:深度有限扩展当前节点后生成的子结点总是置于OPEN表的前端,即OPEN表作为栈,后进先出,使用搜索优先纵深方向发展。
二叉树的宽度优先深度优先用队列和栈做我都能手措[🌹][狗头][🌹]
TODO
启发式搜索
基本概念

评估函数

实现启发式搜索的关键因素和A*算法
启发式搜索的关键因素: - 搜索算法的可采纳性 在存在初始状态到目标节点解答路径的情况下,若一个算法总能找到最短(代价最小)的解答路径,则称该状态空间中的搜索算法具有可采纳性,也叫最优性。 宽度优先算法也是可采纳的,只是效率不高。 - 启发式函数h(n)的强弱及其影响强度。 定义 评价函数的比较
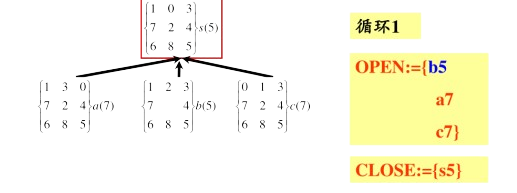
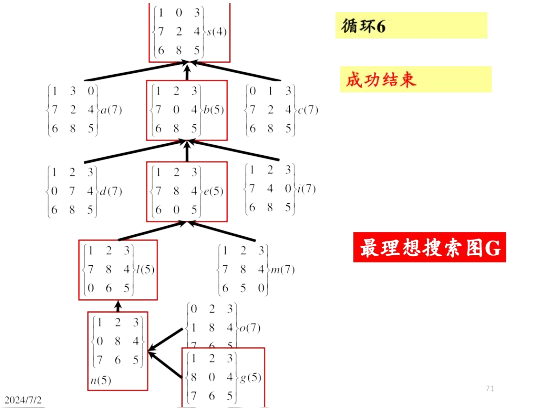
A*算法实例

完整实例: 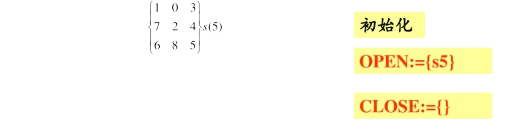
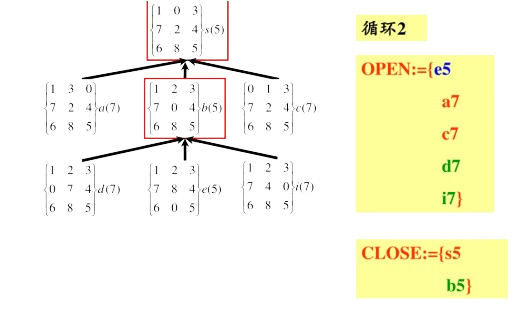
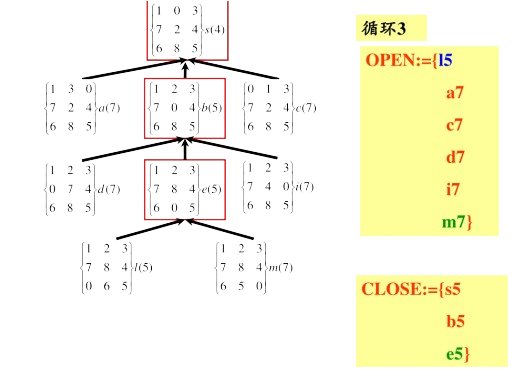
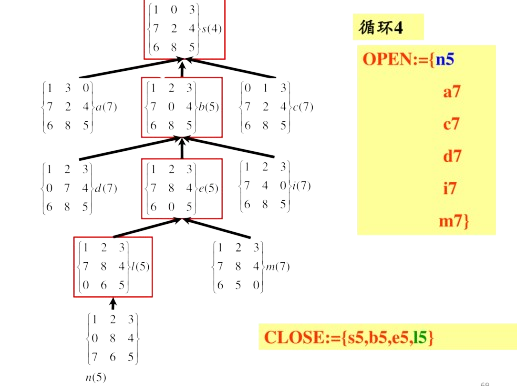
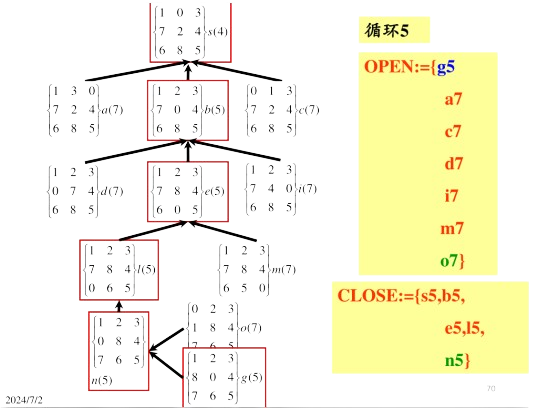
博弈

博弈树
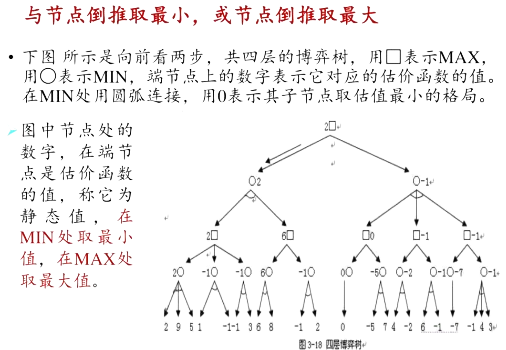
博弈树就是把双人博弈过程用图的形式表现出来,这样就可以得到一个AND-OR树,这种AND-OR树被称为博弈树,博弈树中该MAX走的节点叫做MAX节点,该MIN走的节点叫MIN节点。
两种基本的求解搜索方法 - 极大绩效过程 - a-b过程