人工智能基础确定性推理

确定性推理

推理的基本概念

推理的逻辑基础

谓词公式的永真性和可满足性

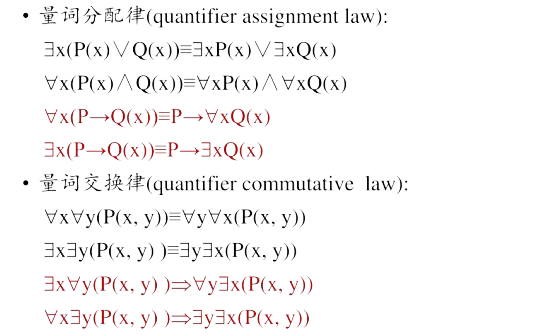## 自然演绎推理

归结演绎推理

子句型

子句与子句集

• 原子谓词公式及其否定都称为文字
• 任何文字的析取都称为子句
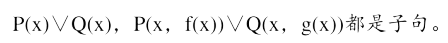
• 不含任何文字的子句称为空子句（空子句永假且不可满足）
• 子句或空子句构成的集合称为字句集

子句集化简

1. 消除连接词” $\to$“和”$\leftrightarrow ︎$”
2. 减少否定符号的辖域:
3. 对变元标准化:在一个量词的辖域内，把谓词公式中收到该量词约束的边缘全部用另外的一个没有出现过的任意变元代替，使用不同量词约束的变元有不同的名字。
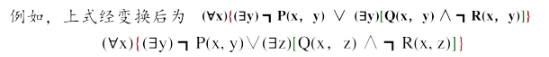
4. 化为前束范式：基于第三步已经对变元标准化，直接将所有的量词都移动到公式的左边，移动时不能改变其相对顺序
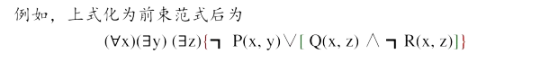
5. 消去存在量词：
   • 若存在量词不出现在全称量词的辖域内（即它的左边没有全称量词）只需要一个新的个体常量替代它即可。
   • 若存在量词位于一个或多个全称量词辖域内，则需要用Skolem函数$f(x_1,x_2,...,x_n)$替换受该量词约束的变元然后再消除该存在量词。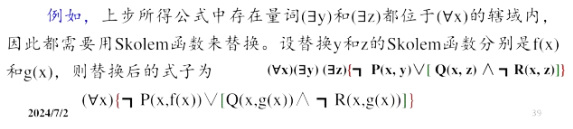
6. 化为SKolen标准型 $$(\mathrm{\forall }{x}_1)...(\mathrm{\forall }{x}_n)M(x_1,x_2,...,x_n)$$ 其中$M(x_1,x_2,...,x_n)$是Skolem标准母式，它由子句的合取构成
7. 省掉全称量词：由于母式中的全部边缘均受到全称量词的约束，并且全称量词的次序无关紧要，因此可以省掉全称量词
8. 根据合取词提取拆分公式：在母式中消去所有的合取词，把母式用字句集的形式表示出来。其中字句集上的每一个元素都是一个子句。
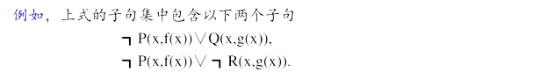
9. 更换变量名称：对子句集中的某些变量重新命名，使任意两个子句中不出现相同的变量名

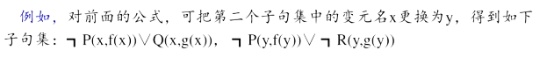
鲁宾逊归结原理

基本思想：